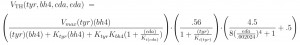In our first investigation into brain physiology, we constructed a mathematical model of dopamine (DA) terminal (Best et al. 2009) so that we could study synthesis, release, and reuptake and the homeostatic mechanisms that control the concentration of DA in the extracellular space. We investigated the substrate inhibition of tyrosine hydroxylase (TH) by tyrosine, the consequences of the rapid uptake of extracellular dopamine by the dopamine transporters, and the effects of the autoreceptors on dopaminergic function. The main focus was to understand the regulation and control of synthesis and release and to explicate and interpret experimental findings. We started with a model of DA terminal because dopamine is known to play an important role in many brain functions. Dopamine affects the sleep-wake cycle, it is critical for goal-directed behaviors and reward-learning, and it modulates the control of movement via the basal ganglia. Cognitive processing, such as executive function and other pre-frontal cortex activities, are known to involve dopamine. Finally, dopamine contributes to synaptic plasticity in brain regions such as the striatum and the pre-frontal cortex.
Dysfunction in various dopaminergic systems is known to be associated with various disorders. Reduced dopamine in the pre-frontal cortex and disinhibited striatal dopamine release is seen in schizophrenic patients. Loss of dopamine in the striatum is a cause of the loss of motor control seen in Parkinson’s patients. Studies have indicated that there is abnormal regulation of dopamine release and reuptake in Tourette’s syndrome and dopamine appears to be essential in mediating sexual responses. Furthermore, microdialysis studies have shown that addictive drugs increase extracellular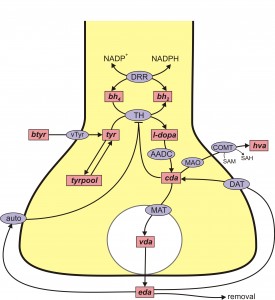
dopamine and brain imaging has shown a correlation between euphoria and psycho-stimulant-induced increases in extracellular dopamine. These consequences of dopamine dysfunction indicate the importance of maintaining dopamine functionality through homeostatic mechanisms that have been attributed to the delicate balance between synthesis, storage, release, metabolism, and reuptake. It is likely that these mechanisms exist both at the level of cell populations and at the level of individual neurons.
A schematic diagram of the mathematical model is given in the figure above that represents a DA terminal. The pink boxes contain the acronyms of substrates and the blue ellipses the acronyms of enzymes and transporters. Each arrow indicates a biochemical reaction, a transport velocity of and influence. Dopamine is synthesized in the nerve terminal from the tyrosine (Tyr) which is transported across the blood brain barrier. We include exchange between tyrosine and a tyrosine pool that represents all the other uses and sources of tyrosine in the terminal. Tyrosine is converted into L-3,4-dihydroxyphenylalanine (l-dopa) by tyrosine hydroxylase (TH) and l-dopa is converted into cytosolic dopamine (cDA) by aromatic amino acid decarboxylase (AADC). cDA inhibits TH and transported into the vesicular compartment by the monoamine transporter (MAT) and vesicular dopamine (vDA) is released from the vesicular compartment into the extracellular space at a rate proportional to the firing rate of the neuron. In the extracellular space, extracellular dopamine (eDA) affects the autoreceptors, is taken up into the terminal by the dopamine transporters (DATs) and is removed from the system by uptake into glial cells and the blood and by diffusion. Dopamine is also catabolized both in the terminal by monoamine oxydase (MA0).
The variables in the mathematical model are the concentrations of the 10 pink boxed substrates. Each differential equations simply reflects mass balance: the rate of change of the concentration of the substrate is the sum of the rates by which it is being made minus the sum of the rates by which it is lost. So, for example, the differential equation for [cDA] is
d[cDA]/dt = VAADC([l-dopa]) + VDAT([eDA]) – VMAO([cDA]) – VMAT([cDA],[vDA]).
Each V is a velocity (a rate) and the subscript indicates which rate. These velocities depend on the current concentrations of one or more of the variables. So, for example, VMAT depends on both [cDA] and [vDA] because there is leakage out of the vesicles back into the cytosol. Similarly the differential equation for [eDA] is
d[eDA]/dt = auto([eDA])fire(t)[vDA] – VDAT([eDA]) – k [eDA].
The first term on the right is release of dopamine into the extracellular space, which depends on the current state of the autoreceptors, auto([eDA]), the current firing rate, fire(t), and the vesicular concentration, [vDA]. The second term is the uptake back into the terminal cytosol and the third term is removal.
Determination of the functional forms of the velocities. Each of the velocities, such as VTH, VAADC, or VDAT depends on the current state of one or more of the variables. How do we determine the functional form of the dependence? If we can, we assume simple Michaelis-Menten kinetics. For example,
VDAT([eDA]) = Vmax[eDA]/(Km + [eDA]).
In other cases the formula might be much more complicated depending on what is known about about how enzymes of transporters are activated or inhibited by molecules that are or are not its substrates. For example the formula for VTH is:
The velocity VTH depends on the current values of its substrates, [tyr] and [bh4], and on [cDA] because it inhibits the enzyme. The first term on the right is standard Michaelis-Menten kinetics with the additional inhibition by cDA. The second term expresses the fact that TH is inhibited by its own substrate, tyr. The last term on the right is the effect of the autoreceptors that depends on eDA. Not so much is known about the mechanism of this effect, so we took a functional form that was consistent with in vitro experiments in the literature.
How are the parameters determined? The answer is, alas, with difficulty. There are measurements of Km values in the literature. Sometimes they vary over two orders of magnitude, which is not surprising because often they are measured in test tubes or in vitro or measured in different cell types under different conditions. There are few Vmax values in the literature because fluxes are hard to measure, especially in vivo. Typically we adjust the Vmax values so that the concentrations at steady state in the model are in the ranges measured experimentally. We take the choice of parameters seriously, and we do the best we can.
But if we don’t know the exact, correct values of the parameters, is the model right? This question (that we frequently get) is based on two misunderstandings. First, there are no exact, correct values of the parameters. In each of us, the parameters are somewhat different, because of genotype, because of environmental inputs, and because of changing gene expression levels. If we do our job well, we can hope to have a dopamine terminal system for an “average’’ person, and it is of course very relevant to ask how the behavior of the system depends on the parameters. Secondly, there’s no “rig
ht” model. Every model is a simplification of a very complicated biological situation. We don’t regard our models as fixed objects, or “right” or “wrong”, but as growing and changing as we learn more from experiments and from computation. The purpose of the model is to have a platform for in silico experiments that will increase our understanding of the biology.
A serotonin terminal model. We created a similar model for a serotonin (5HT) terminal (Best et al. 2010) and have used the DA and 5HT models to study various questions in brain physiology including depression and Parkinson’s disease. References can be found under the publications tab and examples are given under the other tabs under “brain physiology.” Here we content ourselves with two simple examples. The figure above shows the effects of the 5HT autoreceptors. In Panel A the firing rate is varied, in Panel B the activity of the serotonin transporter (SERT) is varied, and in Panel C the activity of tryptophan hydroxylase (TPH) is varied. In Panels B and C, common polymorphisms in the population are shown on the x axis. In each panel, the y-axis shows the concentration of 5HT in the extracellular space at steady state in the model. The green curves show the steady state values in the normal model and the blue curve shows the steady state vales when the autoreceptors are turned. In each case, the variation in extracellular 5HT is much less in the presence of the autoreceptors. This shows how the autoreceptors buffer the extracellular concentration of 5HT against changes in firing rate and gene polymorphisms in two key proteins.
It is interesting that TH, the key enzyme for creating DA, and TPH, the key enzyme for creating 5HT show substrate inhibition. That is, the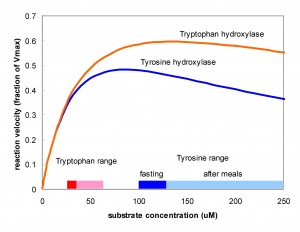 
substrate of the enzyme inhibits the enzyme itself. One can see this in the velocity curves above. Instead of the normal Michaelis-Menten shape where the velocity curve would saturates the curves reach a maximum and then begin to descend. The effect is much stronger for TH than for TPH. Does this matter? Well, that something one can try out using the models. Panel A in the figure below shows (assumed) amino acid curves in the blood for tyrosine and tryptophan due to three daily meals. Panel B shows the tyrosine and tryptophan concentrations in the cytosols of the terminals. Panel C shows the velocities of the TH and TPH reactions. Notice that VTH varies only a little but VTPH varies a lot. Why is that? The normal fasting concentration of tyrosine in the DA cells is 100-125 muM which puts it in the flat part of the VTH curve so changes in tyrosine in the blood and cell don’t change the synthesis rate of DA very much. In contrast, the synthesis rate of VTPH varies quite a bit with the changes in blood and cytosolic tryptophan because the fasting concentration of tryptophan in 5HT cells is on the sharply rising part of the velocity curve. As a consequence, the concentration of 5HT in the vesicles (Panel 4) and the
extracellular space (not shown) varies modestly while the concentration of DA varies very little. In fact, it is known that brain DA is quite insensitive to the protein content of meals but that the brain content of 5HT does vary with meals and these simulations show why. For more information on substrate inhibition, see (Lieb et al. 2010).
