RC Circuits

What is an RC Circuit?

As a reminder, an RC circuit uses a resistor and capacitor, and a capacitor is a circuit component that can store and discharge charge (energy) through a load element [1]. Shown below is the inverse relationship between the resistor and the capacitor, where as time goes on with the RC circuit connected, the charge increases over the capacitor while the current over the resistor decreases. This causes the voltage over the capacitor to increase while the voltage decreases over the resistor.

(a) Charge on the capacitor versus time as the capacitor charges. (b) Current through the resistor versus time. (c) Voltage difference across the capacitor. (d) Voltage difference across the resistor. [1]

Because the voltage increases over the capacitor to an approximate maximum value, you can use that maximum voltage value to figure out the instantaneous amount of power over the capacitor due to that amount of voltage. The amount of power is related to the capacitance (C) and voltage (V) and the equation is shown below.

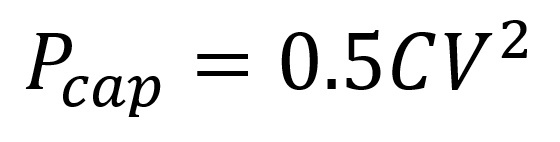
Power over a Capacitor using Maximum Voltage

A key component of an RC circuit is that the capacitor acts as a filter and can smooth out the output voltage. The charged capacitor stores energy and can be passed through a load at a specific frequency level, which is determined by the time constant, or RC value [2]. Your RC value can then determine the cutoff frequency, or the point at which the system’s response will be reduced rather than passed through.

To figure out our RC value for experimentation purposes, we used the cutoff frequency equation, where our frequency was approximated to 60 Hz for our experiments. This was based on our approximation of our rps from the wave generator components and could be changed for future experimentation.

Cutoff Frequency Equation

The larger your input frequency or smaller your RC value, the capacitor will charge and discharge quicker, which allows higher frequencies to pass through, but your overall maximum voltage level is lower. When the input frequency is smaller or the RC value is larger, the capacitor undergoes slower charging and discharging processes. This characteristic enables lower frequencies to pass through, leading to output voltages that closely align with the input signal’s maximum values. 

Filter Affect of an RC Circuit on Output Voltage [3]

By using an RC Circuit, you can use an AC input and store charge on a capacitor. In our experiment, we wanted to find the total voltage and power over our capacitor given an input frequency, input voltage, and desired total RC value, while changing our resistance and capacitance.