About the specific Code, please see Motion-Planning in Github

To Solve the kinematic problem, we need introduce both forward and inverse kinematic problem. We Will start from forward part.

Forward Kinematic

DH Table

When we talk about the kineamtic of Robotic Arm, Denavit-Hartenberg(DH) table is important for both Forward Kineamtic and Inverse Kineamtic.

DH table is DH-Table is a method which could build the model of the robot arm and get the relationship between different joints.

We could see, based on the different angles of joints(assume the length of arms are fixed), we could get a relationship between the start point(base coordinate) and the terminated point(gripper coordinate).

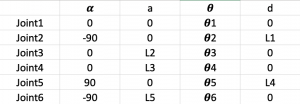
Now we could see a form of our DH table, which is the model of our robot arm.

This DH table includes 4 parameters: α, a, θ, d,  each parameter have different functionality when we model the robot arm. Modified DH

α：The angle that rotate Z axis by the original X axis.

a:    The distance from original Z axis to rotated Z axis following original X axis

θ:   The angle that rotate X axis by the rotated Z axis.

d:   The distance from original X axis to rotated X axis following rotated Z axis.

So based on this parameter, we could describe a complicated robot arm joint by joint. And then, a DH table function, which is also a matrix, could be compuated:

Which is a single matrix for one joint. We just need multiple different transfer matrix for different joints together.

Based on the DH table and our robotic model, we proposed a DH transfer code for solve the forward problem.

Inverse Kinematic

Jacobian Matrix and Gradient Descent

About the Inverse Kinematic, we will combine Jacobian Matrix and DH table to get the Inverse Kinematic.

{\displaystyle \mathbf {J} ={\begin{bmatrix}{\dfrac {\partial \mathbf {f} }{\partial x_{1}}}&\cdots &{\dfrac {\partial \mathbf {f} }{\partial x_{n}}}\end{bmatrix}}={\begin{bmatrix}{\dfrac {\partial f_{1}}{\partial x_{1}}}&\cdots &{\dfrac {\partial f_{1}}{\partial x_{n}}}\\\vdots &\ddots &\vdots \\{\dfrac {\partial f_{m}}{\partial x_{1}}}&\cdots &{\dfrac {\partial f_{m}}{\partial x_{n}}}\end{bmatrix}}.}

the Jacobian Matrix  of a vector-valued function in several variables is the matrix of all its first-order partial derivative. With Jacobian Matrix, we could know the gradient direction of a function(in our problem, it is DH table.)

For instance, in our problem, we know we have such a function:

DH(θ),  θ = (θ1,θ2,θ3,θ4,θ5,θ6 )

Then, with Jacobian Matrix , we could get a gradient of DH, assume it is: ΔDH

Then we change the value of θ, new θ* = θ – λΔDH, here λ is step.

Then the gradient descent until we find the final answer.

The Jacobian Matrix Code could find in Github.

 

Dimension Reduction

But here is a problem: the dimension of six-axis is too large. So it is hard to find a DH value to help us do the Jacobian method and gradient descent. To solve this problem, we proposed a method to reduce the dimension and dof, to make computation more cheap.

 

First we see if in the top view(Z-plant), the arm will hit the obstacles. If not, the robot arm could directly go to grap the objects. If did, we will first find the shortest path in Z-plant, and then solve the motion-planning in XY-plant, which is a 2-dimensional problem.

So now we reduce the dimension and make Jacobian Matrix easily to compute. About the specific compuatation, Will introduce it in RRT part.