As a graduate student, I am interested in synthesizing perspectives from probability and differential equations in order to work on problem in stochastic dynamics, the study of systems that change over time with some degree of randomness. Currently, I am focusing on the following endeavors for my research:
- I am actively engaging with literature on large deviations and hypo-ellipticity to equip me to work on problems that arise from specific stochastic differential equations.
- Over the summer, I organized a probability reading group that met weekly to read and present about logarithmic Sobolev inequalities.
- This fall, I am participating in a variety of reading groups, including one on high-dimensional probability and another on quantum Markovian dynamics.
During undergrad, I participated in two Research Experience for Undergraduates (REU) programs, one of them being at Georgia Institute of Technology and the other being at University of Connecticut.
Past Projects:
University of Connecticut Markov Chains REU (Summer 2022)
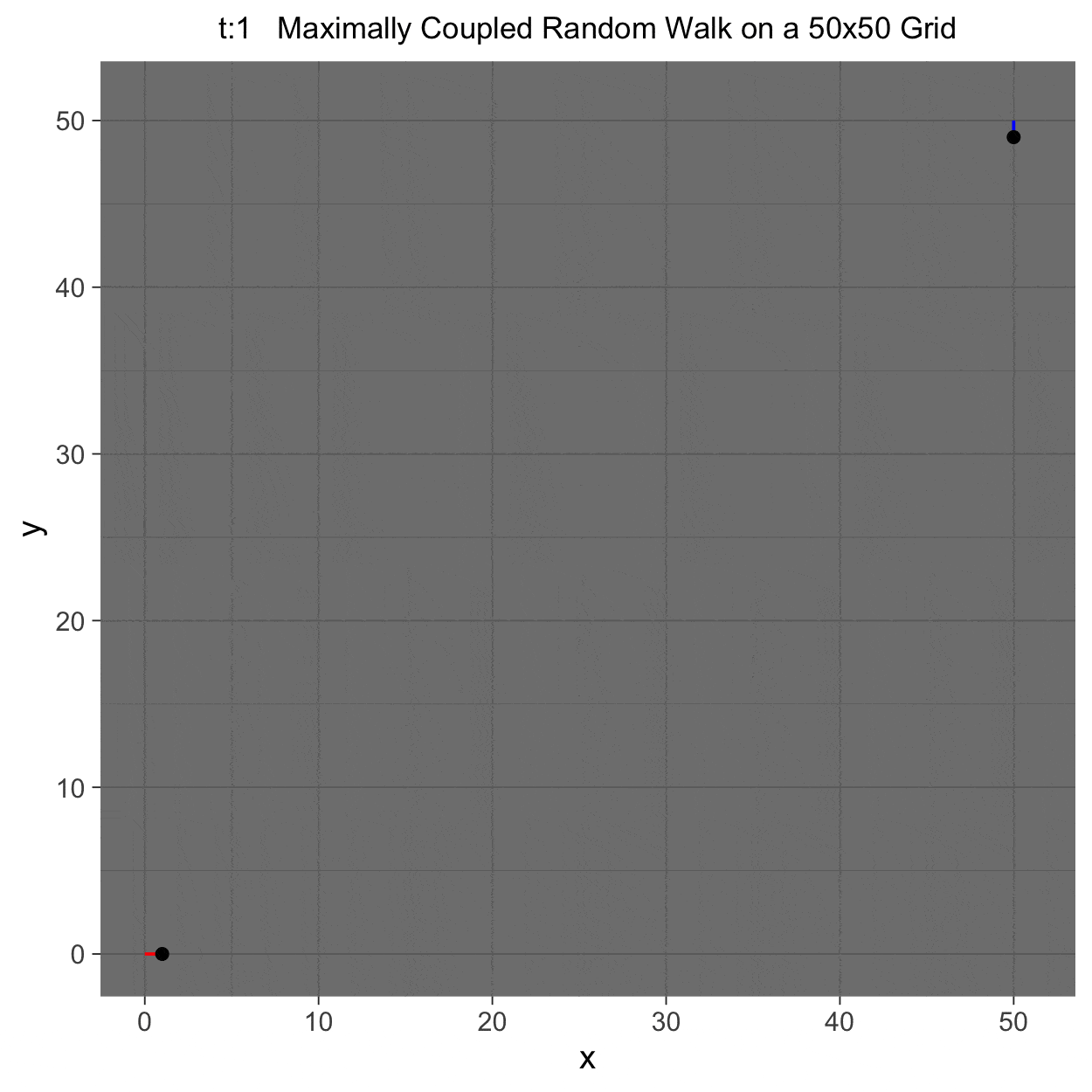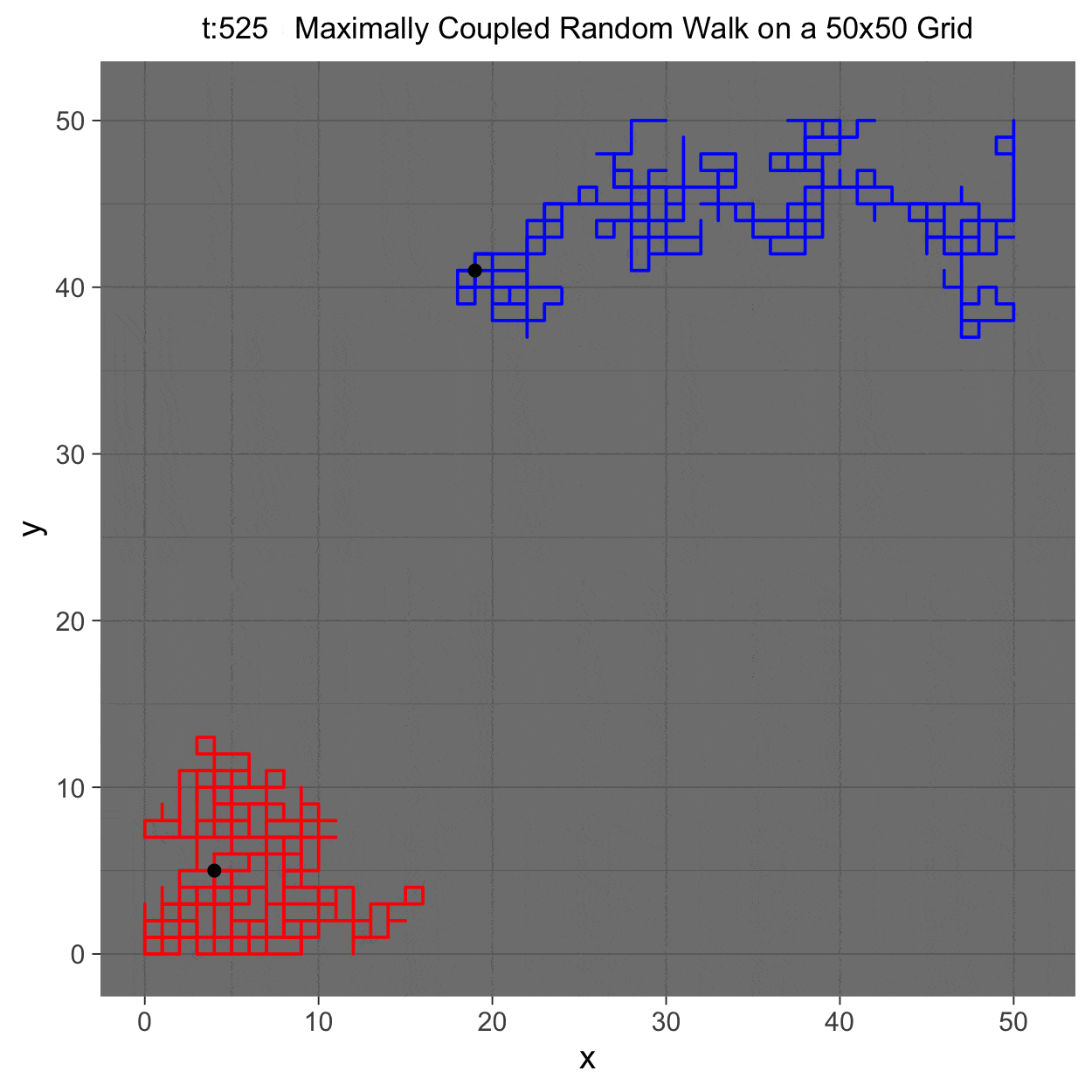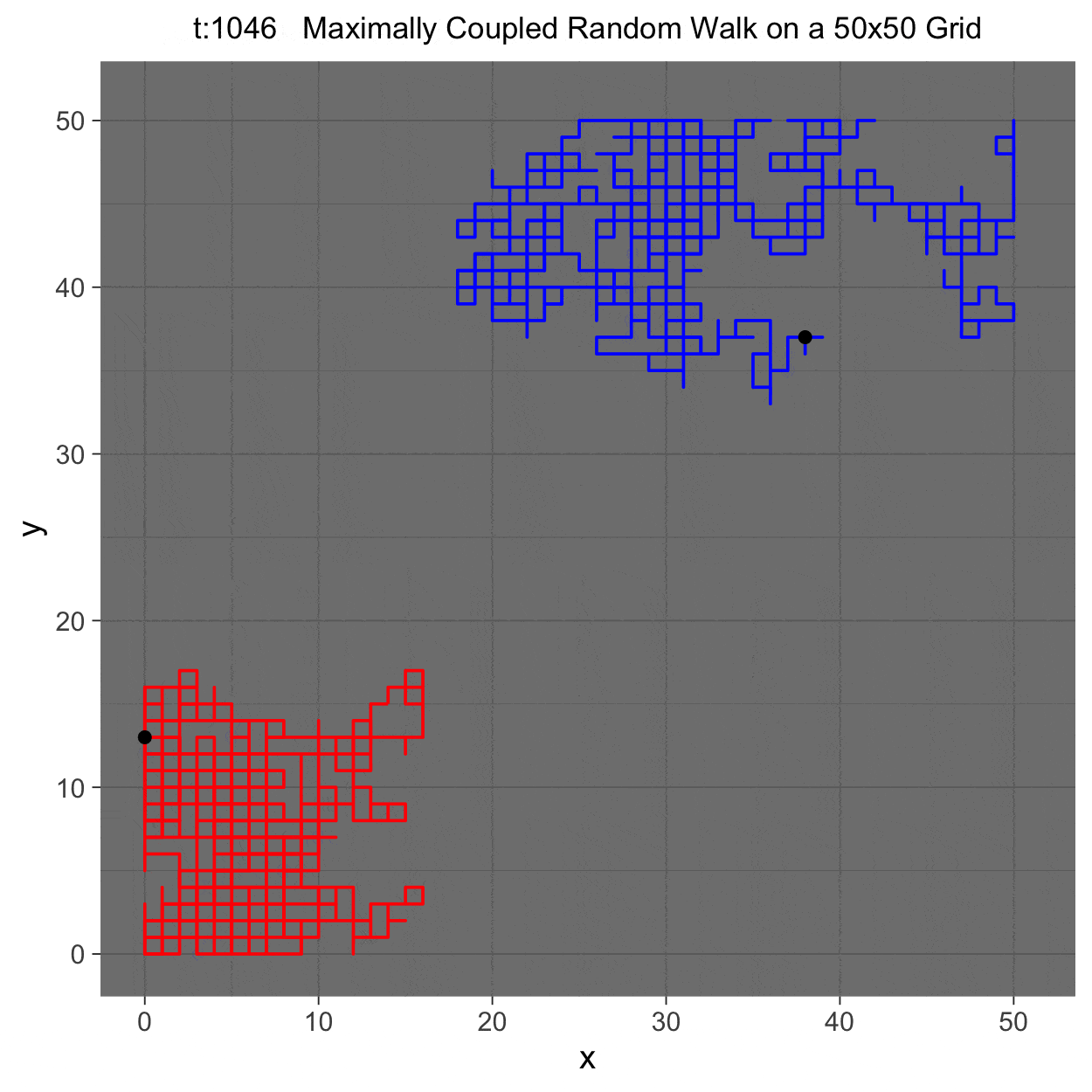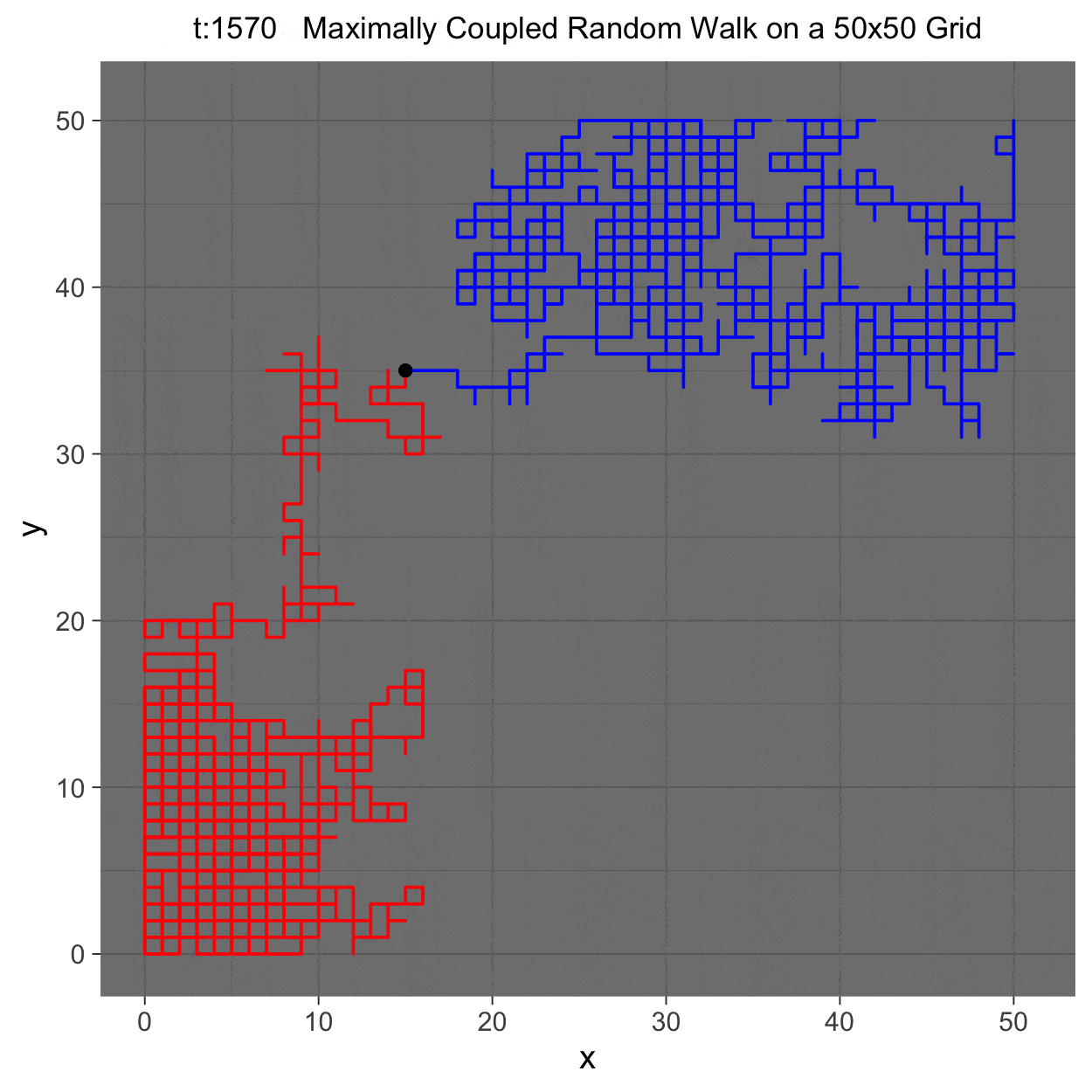
- Advised by Iddo Ben-Ari
- Collaborated with Alan Boles, Leila Dahlia, Bronson Zhou
- Keywords: Markov Chains, Sampling Algorithms
- Link to poster
This REU consisted of many small projects and one large project. Many projects involved reading literature about the applications and theory of Markov processes, though one I particularly enjoyed was discovering a novel proof of the existence of a unique quasistationary distribution for subcritical Galton-Watson processes. The largest project I worked on was developing an algorithm for efficiently sampling maximal couplings of Markov chains. In addition to reading key literature on maximal couplings and adapting past results toward a more algorithmic framework, I implemented the algorithm in a fast program ready to work with high dimensional Markov chains.
We jointly presented the work on maximal couplings via a poster session at the 2023 Joint Mathematics Conference. I also presented it via a talk at Duke’s Graduate-Faculty seminar.
Georgia Institute of Technology Math REU (Summer 2021)
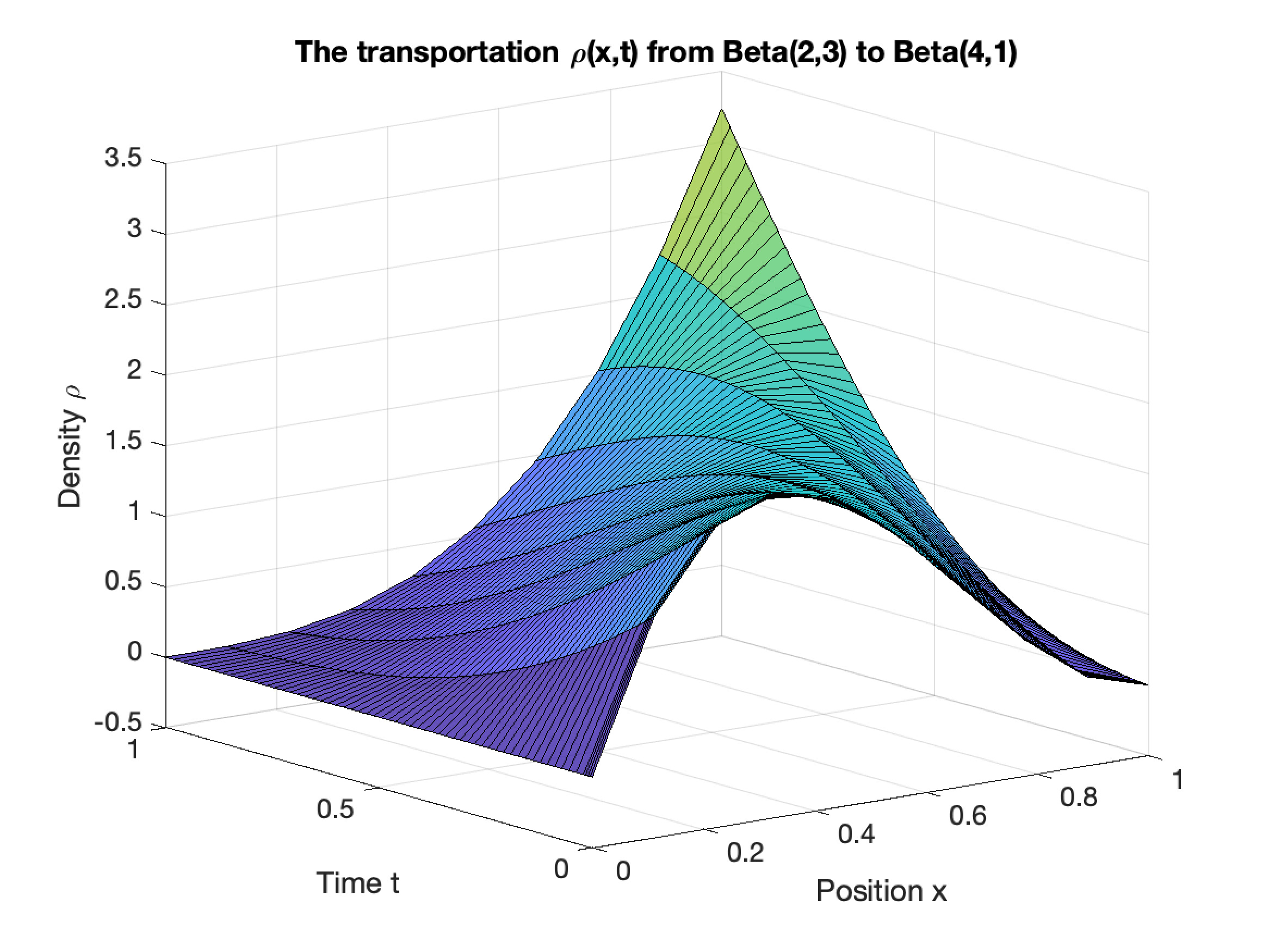
- Advised by Jianbo Cui, Luca Dieci and Haomin Zhou
- Collaborated with Sam Dulin
- Keywords: Numerical Analysis, Optimal Transport
- Link to poster
This REU focused involved researching numerical methods that solve the L^2 optimal transport problem. I translated the optimal transport problem from the classical Monge-Kantorovich formulation to the modern Benamou-Brenier formulation, which allowed us to use spatial discretization, multiple shooting, and homotopy methods to numerically solve the problem. I implemented our algorithm in Matlab and successfully used it to generate graphics.
We jointly presented the work at the REU’s poster session, and then later via a talk at the 2021 Young Mathematician’s Conference at Ohio State University.